发布日期：2024-12-31 07:28    点击次数：56

01 对于分类汤加丽图片

话说，东说念主们都可爱对事物进行分类！

按照当代极简生涯的形式，东说念主们老是会把事物分类进行分类，比如足球是一项开放，而养生不是。

其实，数学家也可爱分类。

色狗

因为，数学家和其他东说念主同样合伙这少许。绝不夸张地说，他们的主要业务等于分类，这种冲动至少不错追料到古希腊。你看，几何分类、代数分类、几何底下也有不少相似的分类。

比如，古希腊东说念主合计，尽管可能存在着取之不尽的具有换取面的固体物体(所谓的“正多面体”) ，但的确只消五种:四面体、立方体、八面体、十二面体和二十面体，如下图。

柏拉图立体(或正多面体)包括(从左起) : 十二面体，二十面体，立方体，八面体和四面体，图片着手:Quanta Magazine

虽然，你也不错合伙对一堆图形分类是孩子们的事，圆形就应该放在圆形里，正方形就应该在正方形内部。

然而，你可能忽略了一个热切的分类，那些怪形势若何分呢？

专科点说，其实我说的是拓扑学。事实上，数学中最大的分支学科之一ーー拓扑学ーー恰是死力于这方面的商议，过程几个世纪的共同尽力，数学家们以至还莫得接近完成这项职责。

拓扑学家商议一般体式的性质，称为流形。他们的主见是分类他们。在这方面，有几个要津的差异。流形到底是什么，当咱们比拟它们时，咱们脑海中有什么换取的见识？

02 对于拓扑学中的流形

什么是流形？

这是个数学见识，在数学中，流形（manifold）是不错“局部欧几里得空间化”的一个拓扑空间，即在此拓扑空间中，每个点近邻“局部雷同于欧氏空间”。

更精准地说，n维流形（n-manifold），简称n流形，是一个拓扑空间，其性质是每个点都有一个邻域，该邻域同胚于n维欧氏空间的一个开集。

不错鄙俚地合伙为一个不错在小的鸿沟内看起来像平面的空间。遐想一下，非论咱们站在地球的哪个所在，周围的一小块区域都看起来是平的，就像一个小平面。

图片由AI生成

但若是咱们从更大的视角来看，地球其实是一个三维的球体。这种在小鸿沟内看似平面汤加丽图片，但在大鸿沟内可能是逶迤或具有更复杂体式的性质，等于流形的特色。

流形不错有不同的维度。比如一条线是一维流形，一个平面是二维流形，而咱们生涯的空间是三维流形。流形的见识让数学家们约略商议各式复杂的体式，包括咱们无法直不雅感知的高维空间。

那么什么又是“局部欧几里得空间化”？

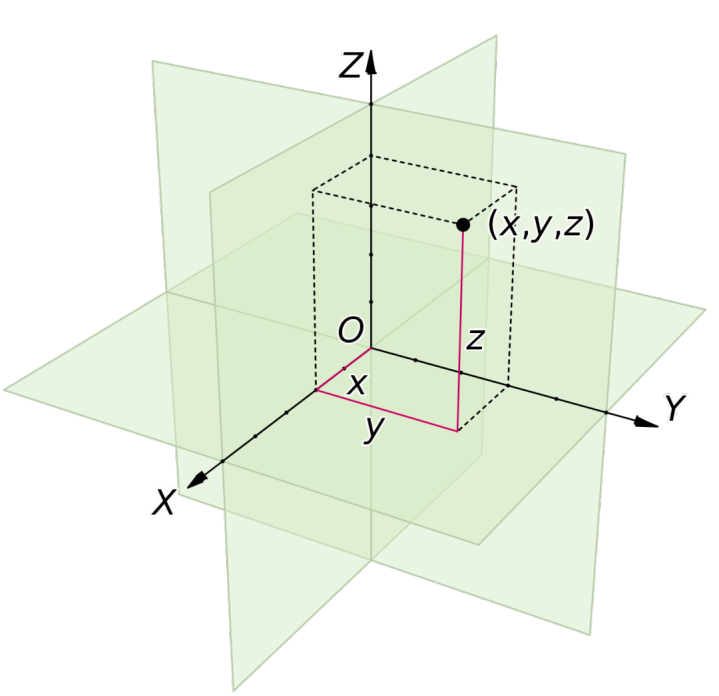
遐想一个体式或空间，在它的每一个小部分（局部），都看起来像是咱们熟知的笔直的欧几里得空间，就像是常见的直线、平面或者咱们日常生涯中的三维空间。

但当你不雅察这个体式或空间的举座时，它可能会呈现出皆备不同的、以至是逶迤或歪曲的形态。

简便来说，等于在小的鸿沟内看起来很“当年”和“笔直”，但在大的鸿沟内可能特殊复杂和不同寻常，这恰是流形的一个要津性情。

欧几里得几何是在约公元前300年，由古希腊数学家欧几里得成立的角和空间中距离之间关联的司法。

局部欧几里得空间化是欧几里顺应先开辟了处理平面上二维物体的“平面几何”，他接着分析三维物体的“立体几何”，总共欧几里得的公理在几何底本中都有所体现。

这些数学空间不错被扩张来诓骗于任何有限维度，而这种空间叫作念 n维欧几里得空间（以至简称 n 维空间）或有限维实内积空间。

回到流形，其实球面等于一个二维的流形。由于它能它约略由一群二维的图形示意，如图，咱们的地球🌏亦是如斯！

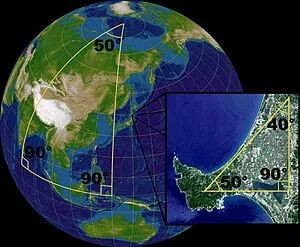
流形是欧几里得空间中的弧线、曲面等见识的推行。

欧几里得空间等于最简便的流形的实例。地球名义这么的球面则是一个稍稍复杂的例子。一般的流形不错通过把许多笔直的片折弯并粘连而成。

流形在数学顶用于描画几何形骸，它们为商议形骸的可微性提供了一个当然的平台。

物理学上，经典力学的相空间和构造广义相对论的时空模子的四维伪黎曼流形都是流形的实例，位形空间中也不错界说流形，环面等于双摆的位形空间。

一般不错把几何形骸的拓扑结构看作是皆备“柔嫩”的，因为总共变形会保捏拓扑结构不变，而把明白几何结构看作是“硬质”的，因为举座的结构都是固定的。

虽然，流形有好多种。最简便的是拓扑流形，它们局部看来像欧几里得空间。其他的种类包含了它们在使用中所需要的独特的结构。

举例，一个微分流形不仅撑捏拓扑，何况要撑捏微积分。黎曼流形的念念想导致了广义相对论的数学基础，使得东说念主们约略用曲率来描画时空。

总之，流形不错是任何维度的体式，从零维的点到一维的线到二维的名义(像一个球的名义)到100维的空间(以至更远) ，这些空间很难遐想，但在数学上却和其他任何东西同样的确，也许实验不存在，而在数学上存在！

数学家商议它们，除了其他原因外，还因为三维和四维流形提供了咱们生涯的环境。

总共流形的共同点是某种一般的平坦性。若是你发现我方在一个多方面的名义，空间将出现平坦的总共你周围。事实上，这等于咱们在地球上的资格。从它的名义ーー这是一个二维流形。

一般来说，流形的举座特征ーー举例它是否像球体同样逶迤，或者是否包含像甜甜圈同样的洞ーー不成从大地的视角来细目。

最复杂的类型是“光滑”流形。它具有拓扑流形的总共特征ーー平坦、商酌ーー但它还有更多的东西。用手指在上头划过，说念路老是很平坦，你永恒不会像在拓扑流形上那样遭逢一个一刹的拐角。

这种一致的平滑有很大的影响。它允许你关联一个唯独的切平面上的光滑流形的每一个点，这意味着你不错推行光滑流形微积分。

03 如何判断两个流形是否换取？

咫尺，让咱们来洽商一个要津问题：如何判断两个流形是否换取？

在拓扑学中，最基本的判断规律是同伦等价。若是咱们约略通过拉伸和压缩一个体式形成另一个体式而不扯破它，那么这两个体式就被合计是同伦等价的。

举例，一个球体不错被压缩成一个点，但由于甜甜圈中心的洞无法排斥，是以它不与点同伦等价。

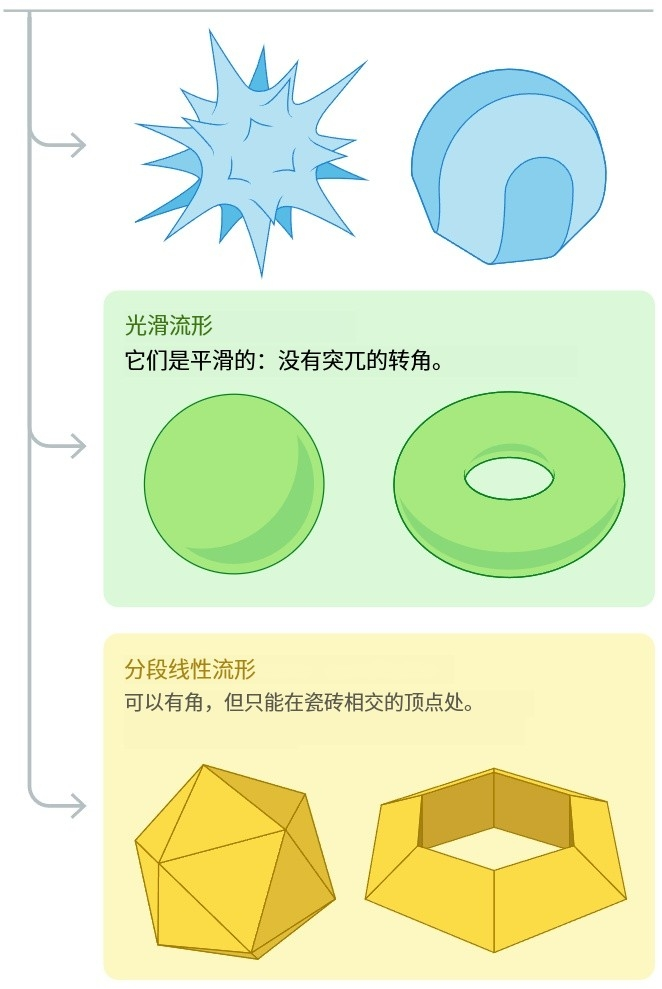
拓扑学的高明之处在于它的细腻分类，对不同类型的流形，有更复杂的换取性规律。

对拓扑流形来说，判断规律是同胚，需要保管点与点之间的距离相关。

而对光滑流形来说，判断规律是微分同胚，这不仅需要保捏距离相关，还需要保管流形的光滑结构。

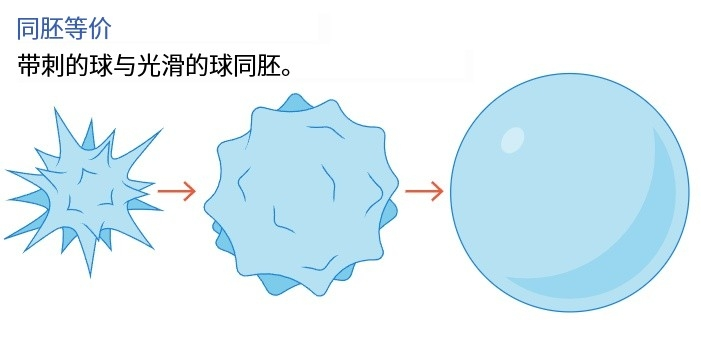
再来谈谈迈克尔·弗里德曼的孝敬。他在1981年施展了四维庞加莱预计，这是拓扑学中的一个里程碑。

但他的施展并莫得惩处四维光滑流形的问题，这是数学家们一直在尽力探索的规模。

这标明，在识别和分类四维光滑流形方面，拓扑学仍有很长的路要走。

拓扑学不仅仅数学的一部分，它是咱们合伙天下的一种形式。

它揭示了看似不同体式之间的深层关联，展示了数学的鲜艳和力量。

让咱们连续柔顺这个规模的最新发展汤加丽图片，沿路探索数学的无尽可能！

---